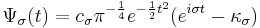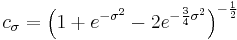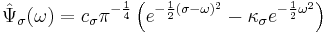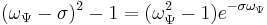Morlet wavelet
In mathematics, the Morlet wavelet, named after Jean Morlet, was originally formulated by Goupillaud, Grossmann and Morlet in 1984 as a constant 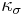 subtracted from a plane wave and then localised by a Gaussian window:
subtracted from a plane wave and then localised by a Gaussian window:
where 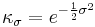 is defined by the admissibility criterion and the normalisation constant
is defined by the admissibility criterion and the normalisation constant 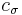 is:
is:
The Fourier transform of the Morlet wavelet is:
The "central frequency" 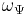 is the position of the global maximum of
is the position of the global maximum of 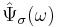 which, in this case, is given by the solution of the equation:
which, in this case, is given by the solution of the equation:
The parameter  in the Morlet wavelet allows trade between time and frequency resolutions. Conventionally, the restriction
in the Morlet wavelet allows trade between time and frequency resolutions. Conventionally, the restriction 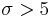 is used to avoid problems with the Morlet wavelet at low
is used to avoid problems with the Morlet wavelet at low  (high temporal resolution).
(high temporal resolution).
For signals containing only slowly varying frequency and amplitude modulations (audio, for example) it is not necessary to use small values of  . In this case,
. In this case, 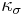 becomes very small (e.g.
becomes very small (e.g. 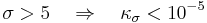 ) and is, therefore, often neglected. Under the restriction
) and is, therefore, often neglected. Under the restriction 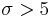 , the frequency of the Morlet wavelet is conventionally taken to be
, the frequency of the Morlet wavelet is conventionally taken to be 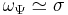 .
.
References
- P. Goupillaud, A. Grossman, and J. Morlet. Cycle-Octave and Related Transforms in Seismic Signal Analysis. Geoexploration, 23:85-102, 1984
- N. Delprat, B. Escudié, P. Guillemain, R. Kronland-Martinet, P. Tchamitchian, and B. Torrésani. Asymptotic wavelet and Gabor analysis: extraction of instantaneous frequencies. IEEE Trans. Inf. Th., 38:644-664, 1992